Kód-optimalizálás php-ban

2013-11-01 kms Programozás

Egy baráti beszélgetés kapcsán jutottam egy érdekes feladat közelébe, amin keresztül a legkülönfélébb optimalizálási technikákat sikerült kipróbálni. Az egyik szépsége, hogy csak php-oldali kód van benne (nincs zavaró html-barkácsolás, illetve futáslassító adatbázis-lekérdezések), így összekeverés nélkül tudtam koncentrálni a programozás algoritmikus szintjére.

A kiírt feladat egyszerű megfogalmazása, valamint a megoldás evolúciója késztetett végül arra, hogy dokumentáljam a folyamatot, ezen keresztül bemutatva a számomra ismert praktikákat.

A feladat

Egy szállodába 25 fős vendégcsoport érkezik. Számoljuk ki, hogy hányféle kombinációban tudunk nekik szállást biztosítani, amennyiben 1, 2, 3 illetve 4 fős szobáink vannak (ezekből korlátlan darabszám áll rendelkezésre), minden szobát teljesen kihasználunk (nincs üres ágy egy kiajánlott szobában sem), valamint nincs kikötés arra sem, hogy ki kivel – vagy kivel nem – szeretne egy szobában lenni.

Korlátaink

A számításnak le kell tudnia futni 1 másodpercen belül egy asztali gépen. A tesztekhez a futtatási korlát 90 másodperc, a memórialimit pedig 128MB.
Én a cikk megírása során tesztgépnek BEORNEGAR-t használtam [Sabertooth X58; Core i7@3.06GHz; 12GB ram; 128GB SSD].

Ízelítő

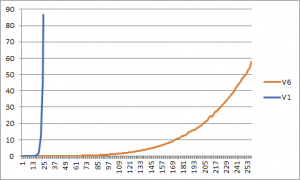
Az alábbi ábrákon az előtte/utána állapotok szerepelnek. Ezzel szeretnék kedvet csinálni a végigolvasáshoz, mivel egy kicsit hosszadalmas. Viszont a görbék azt mutatják, hogy elég sokat sikerült nyerni a leírt technikák alkalmazásával.

A futási idő a vendégek számának függvényében:

Futási idő előtte/utána

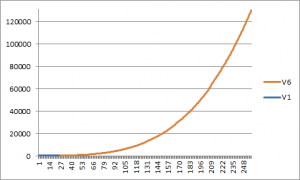
A memóriahasználat ugyanezen aránypárral:

Memóriaigény előtte/utána

Feladatelemzés

A számításhoz fel kell állítani egy modellt. A függvényünknek az alábbi kimenetet kell produkálni:

bemeneti oldalon a vendégek, kimeneti oldalon pedig a variációk száma van

Q₍₁₎ = 1 (egy darab egyfős szoba)
Q₍₂₎ = 2 (egy darab kétfős, és két egyfős szoba)
Q₍₃₎ = 3 (egy darab háromfős, egy két és egy egyfős, illetve három egyfős szoba)
Q₍₄₎ = 5 (rövidítve leírva: 1×4, 1×3+1×1, 1×2+2×1, 2×2, 4×1)

Minden további esetre:
Q_(n) = unique( Q_(n-1) + Q_(n-2) + Q_(n-3) + Q_(n-4) )

Megtéveszthető lehet a unique() függvény egy összeadás eredményére. Ezt azért használtam így, mivel nincs más mód annak jelzésére, hogy a négy különböző függvényfutás által visszaadott variációk közül ki kell ejteni a megegyezőket.

Vegyük sorba a számítási lépéseket, és kiderül miért van erre szükség. Egy és két vendég érkezése esetén nagyon egyszerű fejben is kiszámolni a variációkat, mivel egy vendég esetén egy egyfős, két vendég esetén pedig vagy két egyfős, vagy egy kétfős szobát ajánlunk fel. Három vendég érkezésekor azonban már kezd bonyolódni a helyzet.
Próbáljuk meg három vendégre alkalmazni a Q_(n) függvényt (ahol n > 0):

Q₍₃₎ = Q₍₂₎ + Q₍₁₎ + 1

Amennyiben van n-fős szobánk, abban az esetben plusz egy variációt fel kell jegyeznünk, mivel el tudjuk helyezni az összes vendéget egy szobában.

Az egyenlet lépésenkénti megoldása:
Q₍₃₎ = 2 + 1 + 1
Q₍₃₎ = 4

Ez viszont hibás eredményt ad.

Ha szövegesen követjük a függvények feloldását, akkor meglátjuk miért.

Három vendég érkezése esetén a lehetőségek a következőkből állnak össze:

• egy darab egyfős szoba plusz a két vendégre vonatkozó variációk
• egy darab kétfős szoba plusz az egy vendégre vonatkozó variációk
• egy darab háromfős szoba

Amennyiben végrehajtjuk a rekurzív kibontást:

• egy darab egyfős szoba plusz két darab egyfős szoba
• egy darab egyfős szoba plusz egy darab kétfős szoba
• egy darab kétfős szoba plusz egy darab egyfős szoba
• egy darab háromfős szoba

Itt már jól látszik, hogy az 1×1+1×2 és 1×2+1×1 variációk csak a felírásuk sorrendjében különböznek. Mivel a feladatkiírás szempontjából az, hogy ki kivel alszik egy szobában nem számít, ezért a két kombináció egyenrangú.

Ezekre az ellenőrzésekre vonatkozik a unique() függvény a számítás során, mivel a Q_(n) eredményének meghatározásakor figyelmen kívül kell hagynunk a duplikátumokat.

PHP-kód v1

Mostanra felállítottunk egy elméleti számítási módot, és tudjuk, hogy rekurzív függvényt kell írni. Ezek ismeretében el tudjuk készíteni a kód első változatát.

<?php
  function calc_room_use ($passengers) {
    // a függvény csak pozitív egész számokon értelmezhető
    if ($passengers < 1) {
      return array();
    }
    // ide gyűjtjük majd a lehetséges variációkat
    $variations = array();
    // mind a négyféle szobába megpróbáljuk elosztani a vendégeket
    for ($rn = 1; $rn <= 4; $rn += 1) {
      if ($passengers >= $rn) {
        // kiszámítjuk a Q(n-x) variációkat
        $uplevel_variations = calc_room_use($passengers - $rn);
        $actual_variation = $rn;
        // ez a ciklus felel meg a unique()-nak
        foreach ($uplevel_variations as $variation) {
          // minden variációt egy string-ként tárolunk a tömbben
          $actual_variation = explode(',', $variation);
          // az előző szint variációihoz hozzáírjuk az aktuális szoba méretét
          $actual_variation[] = $rn;
          // sorba rendezzük, hogy a 2,1 és az 1,2 eseteket ki tudjuk szűrni
          sort($actual_variation);
          $actual_variation = implode(',', $actual_variation);
          // és ha nincs ilyen variáció még, akkor felvesszük a lehetségesek közé
          if (! in_array($actual_variation, $variations)) {
            $variations[] = $actual_variation;
          }
        }
        // az egy szobában épp elférünk variációját is fel kell vezetni
        if ($passengers == $rn && ! in_array($rn, $variations)) {
          $variations[] = $rn;
        }
      }
    }
    return $variations;
  }
  // leszámoljuk és kiírjuk a variációkat
  echo count(calc_room_use(25));
?>

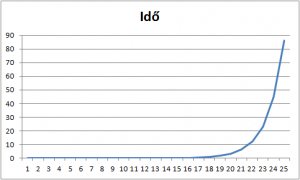
A kód erőforráshasználata diagramon ábrázolva:

Számítási idő

Memóriahasználat

Szöveges értelmezésben:

• 1 másodpercen belül kiszámítható: 18 fő
• 30 másodpercen belül kiszámítható: 23 fő
• 25 fő érkező vendég kiszámítása: 86.33 másodperc
• 128 MB memórialimit elérése: nem a közeljövőben valószínű

Értékelés: szánalmas.

Ezek alapján az első kódverzió nem teljesít a követelménykorlátokon belül, ezért átalakításra szorul. És egyben elkezdődik az evolúciója…

kms

Pages: 1 2 3 4 5 6 7

dinamikus programozás, fejlesztés, optimalizálás, php

MySQL jogosultság-szervezés MAC-alapú kivétel Mikrotik hotspot-ba